Team 8
A Literature Review of Elliptical Curve Cryptography Performance Analysis
Jeremy Turnbull, jaturnbull@uh.edu
University of Houston, College of Technology
Abstract
This paper surveys a series of works that measure the performance benefits of Elliptical Curve Cryptography versus traditional cryptographic algorithms. In these works, ECC is shown to outperform other algorithms in almost every scenario. This paper summarizes these works and offers a few comments regarding their content and presentation.
Keywords – Elliptical Curve Cryptography, literature review, performance analysis, RSA.
I. Introduction
The three tenets of information security are confidentiality, integrity, and availability. Confidentiality refers to keeping information private or a secret; integrity in this context refers to ensuring that no unauthorized party alters the information; and availability refers to being able to access the information when desired. Cryptographic algorithms and systems can assist with the first two of these tenets via encryption and digital signatures, respectively, whereas maintaining availability is a matter of total security and maintenance and is not discussed further in this review.
Cryptography itself can be divided into two broad fields: private-key cryptography and public-key cryptography. Private-key cryptography is also known as symmetric cryptography because both sides of the communication link use the same cryptographic key for all of their processing. This type of cryptography has the advantages of using relatively small keys to produce strong encryption and is therefore quite fast. However, private-key cryptography also suffers from the key exchange problem: that is, how does one share the private-key with the other party over a public and insecure network? One solution is the Diffie-Hellman (D-H) key exchange algorithm, which involves a process that uses random numbers and the discrete logarithm problem to exchange a shared secret. This process is computationally difficult to reverse for an eavesdropper, so it is therefore considered secure. Another method is the use of public-key cryptography, whereby each party uses a public/private key pair for all of their cryptographic operations. In public-key cryptography, the public key is meant to be shared and its security is not a concern, whereas security of the private key is a top priority and it is not intended to be shared with any other party. The public/private key pair can be used together because they are mathematically related but in such a way that the private key cannot be derived from the public key, or at least it is computationally difficult to do so, even with modern computer systems.
The Rivest, Shamir and Adleman (RSA) algorithm was the first publicly-known algorithm that implemented public-key cryptography with strong encryption and that stood the test of time against peer reviewed attacks. In order for RSA to do so, however, it requires the use of relatively large keys. Using such keys is not a problem for modern clients that implement RSA in software and only have to negotiate one secure connection per session; however, for today’s servers that must process hundreds or thousands of connections per second, or for smaller, power-limited devices, having to process cryptographic algorithms using large keys can quickly consume the devices’ resources. In such cases, the device may be forced to use smaller, less secure keys, unless a suitable alternative could be used. One such alternative is the use of Elliptical Curve Cryptography (ECC).
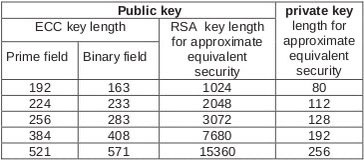
Table 1: Comparison of key sizes for equivalent security [3].
II. ECC Basics
ECC differs from more “traditional” encryption algorithms (like RSA) in that it operates over point addition of an elliptic curve in a prime or binary field rather than modular integer multiplication in an integer field [3]. For a detailed explanation of the previous statement, which is beyond the scope of this document, refer to [4]. Because ECC requires mostly addition operations, computers can execute ECC operations much quicker than RSA operations. Additionally, even though ECC can be implemented as a public-key system, it requires much smaller key sizes than RSA for comparable security. Table 1 shows these key size differences. Because of these two differences (arithmetic operation and key size), ECC outperforms RSA in almost every test.
III. Summary of Reviewed Works
Both [2] and [3] relate to the performance benefits of implementing ECC in hardware, whether it be a CPU instruction set extension as in [2], or a limited resource, embedded environment as in [3]. On the other hand, [5] and [6] explore the benefits of substituting ECC into common cryptographic algorithms used in modern software to secure World Wide Web transactions. Finally, [7] discusses how ECC can also improve the speed and security of email. Throughout the remainder of this section, each paper is identified in a section heading by an abbreviated version of its title.
A. ARM ISA Extension
The goal of [2] is to determine whether an extension to the instruction set of an ARM Central Processing Unit (CPU) would improve the processing of cryptographic algorithms, especially those using ECC. The authors mention that, because of the intensity of cryptographic processing, some hardware vendors have included specialized co-processors in their products, intended for servers that expect to perform a large number of cryptographic operations per second. Adding a separate co-processor, however, is relatively expensive, especially on systems for which the ARM CPU is intended (low power, limited resource). Therefore, the authors profess that extended the instruction set of a common processor is the better approach.
The authors used the sim-profile and sim-outorder programs from the SimpleScalar tool set to simulate and measure the results of adding an instruction for word-level, polynomial multiplication in binary finite fields in a CPU modeled after the Intel XScale architecture. The authors conclude that such an addition results in a 33% reduction of total instructions executed with a load consisting of cryptographic operations. Note that a separate instruction would be needed in order to achieve similar results when operating within a prime finite field. In order to reach these conclusions, the authors used a version of the MIRACL C library that they modified in order to create a benchmark testing suite consisting of the ECC versions of the D-H, Digital Signature Algorithm (DSA), and ElGamal algorithms that recognized the new instruction. Although the only factor of the test was the ECC key size at levels 163, 233, 283, 409, and 571 bits, the influence of two other metrics, namely the usage of a zero cache size and projective coordinates, were verified to not be significant by comparing the previous results using varying cache sizes and affine coordinates.
Figure 1: Example of chart cluttering in [2]. This image was taken at 100% zoom level.
Finally, a few statements concerning the various charts and graphs within the paper. First, all of the graphics in this paper were in color, which made trying to discern the various categories or series in the graphic that much easier as compared to the graphics of the other works reviewed in this paper. However, all of the graphics only spanned the width of a column instead of the entire page and contained so many categories or levels that they were still difficult to read, especially at a scale as printed on a page (Fig. 1).
B. Workload Characterization
This paper shares many similarities with the previous one due in no small part to the fact that all of the authors of this paper also contributed to the previous. Other common traits include the usage of a simulated CPU based on the Intel XScale® architecture, the MIRACL C library to create suitable benchmarks, and the SimpleScalar tool set for measurement. However, this paper was published one year before [2], and its goal is to compare the performance of various ECC methods in a simulated, embedded environment. At first, the authors only measured the number and type of instructions executed to perform cryptographic operations using various ECC-modified and unmodified algorithms with equivalent-security key lengths as workloads. Measuring such responses, the authors found that the ECC-modified algorithms use roughly 10-60% fewer instructions than their unmodified counterparts. However, when the authors also measured execution times, they initially discovered that RSA performed better than ECC, which theoretically should not happen. To explain why, the same workloads were used against varying memory parameters (branch prediction scheme, latency, and cache size). The authors give a detailed description of how memory configurations affect execution time of cryptographic operations. Additionally, all tests and results were compared against similar tests using the MiBench/Security suite for control.
Just as in [2], the authors once again use graphics that seem too small for the amount of information they are attempting to convey. Worse yet, the graph legends use gray-scale shadings that are difficult to distinguish in non-color print. The use of various hash patterns, as used in the next two papers, would have been a better choice.
C. ECC for SSL
The goal of [5] was to determine specifically how much ECC can improve the performance of establishing a Secure Sockets Layer (SSL) session. In order to determine this value, the authors measured the handshake cryptographic latency and the server cryptographic throughput. In this context, the latency is defined as the total amount of time spent processing cryptographic operations in both the client and server, and the throughput is defined as the rate at which the server can perform cryptographic handshake operations (measured in terms of handshakes per second). The tests were performed using two different systems: Yopy, a Linux-based Personal Digital Assistant (PDA) with a 200MHz processor and wireless connection, and a Sun Ultra-80 server with a 450MHz UltraSPARC II processor. Therefore, three difference scenarios were run: Yopy to Yopy (mimicking a peer-to-peer connection), Yopy to Ultra-80 (mimicking a wireless device requesting a secure Web page), and Ultra-80 to Ultra-80 (mimicking a typical client-server interaction). In each scenario, ECC was compared directly to RSA, varying only whether to use client authentication and two different key sizes of comparable cryptographic strength (163ECC/1024RSA and 193ECC/2048RSA). The tests were measured using the OpenSSL speed program. The tests show that ECC significantly outperforms RSA in all cases.
Most of the figures for the results of this paper were placed at the end, almost like an appendix. This author has found that placing these figures in this location makes reading the text much easier due to the absence of in-line graphics splitting the text in odd ways. Additionally, finding each figure seemed easier as well because they were all in one place. Finally, as mentioned in Workload Characterization, the graphics in this paper use hash patterns to distinguish series, which makes understanding them in black and white print much easier.
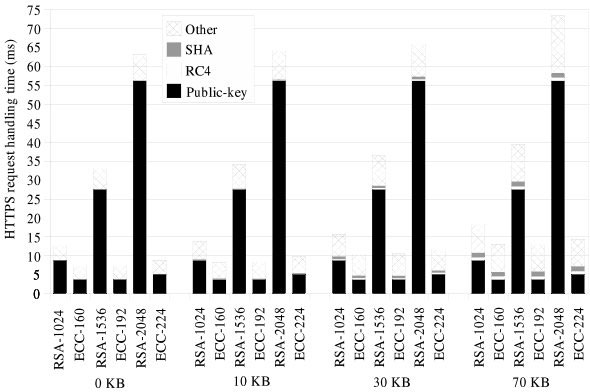
Figure 2: Relative costs in an HTTPS transaction for different file sizes [6].
D. Secure Web Transactions
This paper [6] is the follow-up to that in ECC for SSL, and therefore the goal is the same. However, in this paper the responses measured are the first response time and fetches per second, where the former is defined as the delay in initiating a request and receiving the first reply packet, and the latter as the rate at which the server fulfills Web page requests, measured in pages per second, with a page defined as an HTML file and all referenced images. Additionally, the authors have greatly increased the workload by using the Badia survey [1] as input. This survey is a trace of real-world network traffic to six, high-demand, secure Web sites. The trace was executed in parallel using the open-source http_load tool against an Apache Web server and measured once again by using the OpenSSL speed program. Another significant change from the tests in [5] is the testing of many more scenarios. The factors in this paper’s tests include two different cipher suites, three different key sizes, three different ECC prime field curves, four different files sizes, and four different session reuse models, for a total of 288 scenarios. For reasons of obvious space limitations, not all results were shown in the paper, yet Fig. 2 shows the results of many of these tests. As can be seen in this figure, ECC once again outperforms RSA in each case, with the difference growing exponentially with larger key sizes.
E. Wireless Security
In this final paper [7] the author references the results of some of the papers mentioned above as well as others to extrapolate what the results would be if the same workloads were used against a Secure Multipurpose Internet Mail Extensions (S/MIME) server in a wireless environment. The author of this paper does an excellent job of explaining many of the concepts of cryptography, ECC, RSA, and others, but does not conduct any tests of her own. Therefore, this author found the title and abstract of [7] to be misleading.
IV. Conclusion
The works reviewed in this paper all show that ECC outperforms RSA at every measurement in almost every scenario. However, an aspect that has bothered this author throughout reviewing these works is that each of these papers’ authors have tested ECC versus RSA using equivalently strong key sizes. Although this decision makes sense for the sake of a control, given that ECC uses an equivalently much smaller key size than RSA, the results should be obvious. As a matter of due diligence, this author would liked to have also seen these same tests conducted using the same key size for RSA and ECC in order to determine how much of the performance benefit is due to the key size and how much is due to the specific algorithm or implementation. Granted, in such a scenario the cryptographic strength of RSA would be greatly reduced, less than that of ECC, and would not be suitable for real-world applications; however, the effect of each factor would be known.
References
- L. Badia. (2001, Sept.). Real World SSL Benchmarking. Rainbow Technologies.
- S. Bartolini, I. Branovic, R. Giorgi, and E. Martinelli, “A Performance Evaluation of ARM ISA Extension for Elliptic Curve Cryptography over Binary Finite Fields,” in 16th Symp. Computer Architecture and High Performance Computing, 2004, pp. 238-245.
- I. Branovic, R. Giorgi, and E. Martinelli, “A workload characterization of elliptic curve cryptography methods in embedded environments,” in MEDEA ’03 Proc. 2003 workshop MEmory performance: DEaling with Applications, systems and architecture, New York.
- Digital Signature Standard (DSS), FIPS Standard 186-3, 2009.
- V. Gupta, S. Gupta, S. Chang, and D. Stebila, “Performance analysis of elliptic curve cryptography for SSL,” in WiSE ’02 Proc. 1st ACM Workshop Wireless security, Atlanta, GA.
- V. Gupta, D. Stebila, S. Fung, S. C. Shantz, N. Gura, and H. Eberle, “Speeding up Secure Web Transactions Using Elliptic Curve Cryptography,” in Proc. Network and Distributed System Security Symp., 2004.
- K. Lauter, “The advantages of elliptic curve cryptography for wireless security,” Wireless Communications IEEE, vol. 11, no. 1, pp. 62-67, Aug. 2004.